10142. Сила времени

Вы должны завершить n процессов. Все номера процессов уникальны и принимают значения от 1 до n. Вам заданы две вещи:

· Порядок, в котором процессы будут вызываться на выполнение.

· Идеальный порядок, в котором все процессы должны были быть выполнены.

Если процесс, вызванный на выполнение, не может быть выполнен (не подходит под идеальный порядок), то его ставят в конец очереди вызова на выполнение.

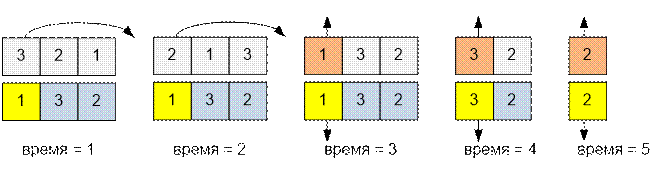
Продемонстрируем это на примере. Допустим, имеются 3 процесса с порядком вызова 3 – 2 – 1 и идеальным порядком 1 – 3 – 2. Процесс номер 3 сможет быть выполнен только после завершения процесса 1, процесс 2 сможет быть выполнен только после выполнения процесса 3.

· Итерация #1: Согласно идеальному порядку первым на выполнение должен поступить процесс #1, однако на выполнение поступает процесс 3. Порядок на выполнение изменяется: первый элемент перемещается в конец. Изменение положения элемента занимает 1 единицу времени. Новый порядок на выполнение примет вид: 2 – 1 – 3. Время на шаг #1: 1.

· Итерация #2: Согласно идеальному порядку первым на выполнение должен поступить процесс #1, однако на выполнение поступает процесс 2. Порядок на выполнение изменяется: первый элемент перемещается в конец. Новый порядок на выполнение примет вид: 1 – 3 – 2. Время на шаг #2: 1.

· Итерация #3: Первый элемент в порядке на выполнение совпадает с первым элементом в идеальном порядке. Процесс #1 выполняется и удаляется из очереди. Время на шаг #3: 1.

· Итерация #4: Поскольку снова первые элементы в порядке выполнения и в идеальном порядке совпадают, то выполняем процесс 3. Время на шаг #4: 1.

· Итерация #5: Последние оставшиеся элементы в обоих порядках идентичны, выполняем процесс 2. Время на шаг #5: 1.

Общее время: 5 единиц.

Выполнение процесса занимает 1 единицу времени. Изменение позиции занимает 1 единицу времени.

Вход. Первая строка содержит количество процессов n (1 ≤ n ≤ 100). Вторая строка содержит порядок в котором процессы будут вызываться на выполнение. Третья строка содержит идеальный порядок, в котором процессы должны выполняться.

Выход. Выведите общее время, необходимое для выполнения всей очереди процессов.

Пример входа	Пример выхода
3 3 2 1 1 3 2	5

РЕШЕНИЕ

очередь

Анализ алгоритма

Объявим две очереди:

· order содержит порядок процессов, в котором они будут вызываться на выполнение.

· ideal содержит идеальный порядок, в котором процессы должны быть выполнены.

queue<int> order, ideal;

Далее следует промоделировать работу очередей:

· Если номер процесса в голове очереди выполнения совпадает с номером процесса в голове идеальной очереди, то выполняем процесс и удаляем его из обеих очередей.

· Иначе следует извлечь процесс из головы очереди на выполнение и поставить его в конец этой очереди.

Пример

Промоделируем выполнение трех процессов из примера.

Реализация алгоритма

Объявим две очереди:

· order содержит порядок процессов, в котором они будут вызываться на выполнение.

· ideal содержит идеальный порядок, в котором процессы должны быть выполнены.

queue<int> order, ideal;

Читаем количество процессов n. Читаем порядки order и ideal.

scanf("%d", &n);

for (i = 0; i < n; i++)

{

scanf("%d", &x);

order.push(x);

}

for (i = 0; i < n; i++)

{

scanf("%d", &x);

ideal.push(x);

}

В переменной res подсчитываем время выполнения процессов.

res = 0;

Продолжаем, пока не будут обработаны все процессы.

while (!ideal.empty())

{

res++;

Если номер процесса в голове очереди выполнения совпадает с номером процесса в голове идеальной очереди, то выполняем процесс и удаляем его из обеих очередей.

if (order.front() == ideal.front())

{

order.pop();

ideal.pop();

}

else

{

Иначе следует извлечь процесс из головы очереди на выполнение и поставить его в конец этой очереди.

x = order.front(); order.pop();

order.push(x);

}

}

Выводим ответ.

printf("%d\n", res);

Java реализация

import java.util.*;

public class Main

{

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

Queue<Integer> order = new LinkedList<Integer>();

for (int i = 0; i < n; i++)

{

int x = con.nextInt();

order.add(x);

}

Queue<Integer> ideal = new LinkedList<Integer>();

for (int i = 0; i < n; i++)

{

int x = con.nextInt();

ideal.add(x);

}

int res = 0;

while (!ideal.isEmpty())

{

res++;

if (order.peek() == ideal.peek())

{

order.poll();

ideal.poll();

}

else

{

int x = order.poll();

order.add(x);

}

}

System.out.println(res);

con.close();

}

}